问题
选择题
已知：a、b是正数，且a+b=2，则
|
答案
∵a，b均为正数，a+b=2，b=2-a，
设W=
+a2+1
=b2+4
+a2+1
，(2-a)2+22
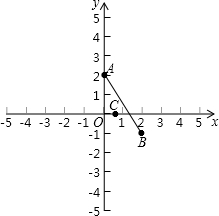
从上式可以看出：W表示x轴上一点C（a，0）到A（0，2），B（2，-1）的距离之和，
最小值为AB=
（注意取值范围：0＜a＜2），13
∴W最小值=
，13
故选A．
搜题请搜索小程序“爱下问搜题”
已知：a、b是正数，且a+b=2，则
|
∵a，b均为正数，a+b=2，b=2-a，
设W=
+a2+1
=b2+4
+a2+1
，(2-a)2+22
从上式可以看出：W表示x轴上一点C（a，0）到A（0，2），B（2，-1）的距离之和，
最小值为AB=
（注意取值范围：0＜a＜2），13
∴W最小值=
，13
故选A．