在平面直角坐标系中，已知三点A（0，a），B（b，0），C（b，c），其中a，b，c满足关系式|a-2|+（b-3）2=0，c=2b-a；
（1）求a，b，c的值．
（2）如果在第二象限内有一点P（m，1），请用含m的式子表示四边形ABOP的面积；若四边形ABOP的面积与△ABC的面积相等，请求出点P的坐标；
附加题：
（3）若B，A两点分别在x轴，y轴的正半轴上运动，设∠BAO的邻补角的平分线和∠ABO的邻补角的平分线相交于第一象限内一点Q，那么，点A，B在运动的过程中，∠AQB的大小是否会发生变化？若不发生变化，请求出其值，若发生变化，请说明理由．
（4）是否存在一点N（n，-1），使AN+NC距离最短？如果有，请求出该点坐标，如果没有，请说明理由．
（1）∵|a-2|+（b-3）2=0，
∴a-2=0，b-3=0，
解得a=2，b=3．
将a=2，b=3代入c=2b-a，得
c=2×3-2=4．
故a=2，b=3，c=4；
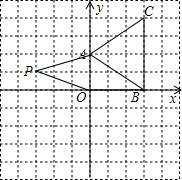（2）如图．如果在第二象限内有一点P（m，1），
那么四边形ABOP的面积=△AOP的面积+△AOB的面积
=
×2×（-m）+1 2
×3×21 2
=3-m；
∵△ABC的面积=
×4×3=6，1 2
∴3-m=6，解得m=-3，
∴点P的坐标（-3，1）；
附加题：
（3）如图．∠AQB的大小不会发生变化，理由如下：
∵∠BAO的邻补角的平分线和∠ABO的邻补角的平分线相交于第一象限内一点Q，
∴∠1=
∠DAB，∠2=1 2
∠ABE，1 2
∴∠AQB=180°-（∠1+∠2）
=180°-
（∠DAB+∠ABE）1 2
=180°-
（90°+∠ABO+90°+∠BAO）1 2
=180°-
（90°+90°+90°）1 2
=45°．
∴∠AQB的大小不会发生变化；
（4）存在一点N（
，-1），使AN+NC距离最短．理由如下：9 8
如图，作出点A（0，2）关于直线y=-1的对称点A′（0，-4），连接A′C，交直线y=-1于点N，则AN+NC距离最短．
设直线A′C的解析式为y=kx+t，
将点A′（0，-4），C（3，4）代入，
得
，t=-4 3k+t=4
解得
，k= 8 3 t=-4
所以直线A′C的解析式为y=
x-4，8 3
当y=-1时，
x-4=-1，8 3
解得x=
，9 8
即点N的坐标为（
，-1）．9 8
故存在一点N（
，-1），使AN+NC距离最短．9 8