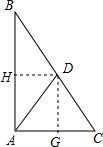
过D作DH⊥AB于点H，作DG⊥AC于点G．

∵在Rt△ABC中，∠BAC=90°，sinB=

5

5

，BC=a，

∴AC=

5

5

a，AB=

2 5

5

a，

∵S_△ABC=

1

2

AB•AC=

a2

5

，

由折叠的性质可得：AD平分∠CAB，

∴DH=DG，

设DH=x，

∴S_△ABC=S_△DAC+S_△ABD=

1

2

AB•DH+

1

2

AC•DG=

1

2

DH（AB+AC）=

1

2

•x•（

5

5

a+

2 5

5

a）=

3 5

10

ax，

∴

3 5

10

ax=

a2

5

，

解得：x=

2 5

15

a，

∴DH=AH=

2 5

15

a，

∴BH=AB-AH=

4 5

15

a，

∴BD=

DH2+BH2

=

2

3

a．

故答案为：

2

3

a．