问题
填空题
已知A(-2,3),B(3,1),P点在x轴上,且|PA|+|PB|最小,点P的坐标是______.
答案
作B关于x轴的对称点C,连接AC,与x轴交于P点,作AD⊥x轴与D.
根据轴对称图形的性质,由图可知,AP+BP=AP+PC,根据两点之间线段最短,P即为|PA|+|PB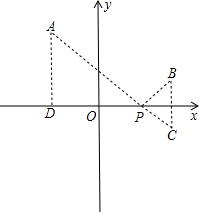 |的最小值点.
|的最小值点.
易得,△ADP∽△CBP,
则
=AD CB
.DP BP
设PB的长为x,则
=3 1
,5-x x
解得x=
,5 4
OP=3-
=5 4
.7 4
可得P点坐标为(
,0).7 4
故答案为:(
,0).7 4

