问题
选择题
设直线 ax+by+c=0的倾斜角为α,且sin α+cos α=0,则a,b满足( )
A.a+b=1
B.a-b=1
C.a+b=0
D.a-b=0
答案
答案:D
由sinα+cosα=0,我们易得tanα=-1,即函数的斜率为-1,进而可以得到a,b的关系.
解:∵sinα+cosα=0
∴tanα=-1,k=-1,-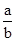 =-1,a=b,a-b=0
=-1,a=b,a-b=0
故选D.
设直线 ax+by+c=0的倾斜角为α,且sin α+cos α=0,则a,b满足( )
A.a+b=1
B.a-b=1
C.a+b=0
D.a-b=0
答案:D
由sinα+cosα=0,我们易得tanα=-1,即函数的斜率为-1,进而可以得到a,b的关系.
解:∵sinα+cosα=0
∴tanα=-1,k=-1,-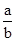 =-1,a=b,a-b=0
=-1,a=b,a-b=0
故选D.