问题
计算题
相距为L的光滑平行导轨与水平面成θ角放置,上端连电阻R,处在与所在平面垂直的匀强磁场中,磁感应强度大小为B0,电阻为r的导体MN(质量m)垂直导轨并在两导轨上,导体MN距离上端电阻R的距离也为L。(设B0=1T,L=1m,θ=30°,m=0.1kg,R=0.8Ω,r=0.2Ω,g=10m/s2)
(1)静止释放导体MN,求:
①MN获得的最大速度vm;
②若MN沿斜面下滑0.2m时恰好获得最大速度,求在此过程中回路一共生热多少焦?

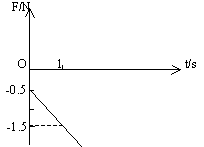
(2)设单位时间内磁感应强度增加量为k,磁感应强度初始值为B0。现给一个平行斜面且垂直MN的外力(设沿斜面向上为外力的正方向),使导体MN始终静止在轨道上。写出外力F随时间t的变化关系式并画出F(沿斜面向上为正)随时间t的函数图象(k=1T/s)。

答案
解:(1)如图:
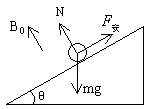
①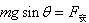 时,速度最大为vm
时,速度最大为vm
而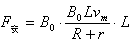
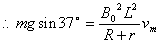
即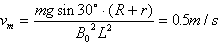
②由能量守恒定律: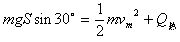
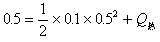
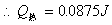
(2)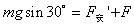
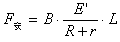
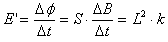
F=0.5-k=-0.5-t