问题
解答题
已知a∈R，
命题p：实系数一元二次方程x2+ax+2=0无实根；
命题q：存在点（x，y）同时满足x2+y2=4且（x+a）2+y2=1；
试判断：命题p是命题q的什么条件（充分、必要、充分不必要、必要不充分、充要或既不充分也不必要条件）？请说明你的理由。
答案
解：若命题p为真，可得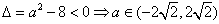
；
若命题q为真，可知圆
有交点，
于是由图形不难得到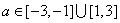
；
若令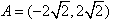集合
，集合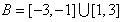
，
可知集合A和集合B之间互不包含，
于是命题p是命题q的既不充分也不必要条件。