问题
解答题
已知三点A(m-1，2)、B(1，1)、C(3，m2-m-1)，若AB⊥BC，求m的值。
答案
解：设AB、BC的斜率分别为k1、k2，
则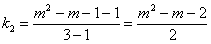
，
又知xa-xb=m-2，
①当m-2=0，即m=2时，k1不存在，此时，k2=0，则AB⊥BC；
②当m-2≠0，即m≠2时，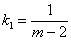
，
由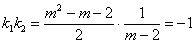
，得m=-3，
故若AB⊥BC，则m=2或m=-3。
搜题请搜索小程序“爱下问搜题”
已知三点A(m-1，2)、B(1，1)、C(3，m2-m-1)，若AB⊥BC，求m的值。
解：设AB、BC的斜率分别为k1、k2，
则，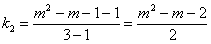
又知xa-xb=m-2，
①当m-2=0，即m=2时，k1不存在，此时，k2=0，则AB⊥BC；
②当m-2≠0，即m≠2时，，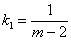
由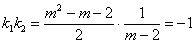，得m=-3，
故若AB⊥BC，则m=2或m=-3。