搜题请搜索小程序“爱下问搜题”
问题 选择题
在矩形ABCD中，AB=1，AD=
3
，P为矩形内一点，且AP=
3
2
，若
AP
=λ
AB
+μ
AD
（λ，μ∈R），則λ+
3
μ的最大值为（　　）
A．
3
2
B．
3+
3
4
C．
6
2
D．
6
+3
2
4
答案

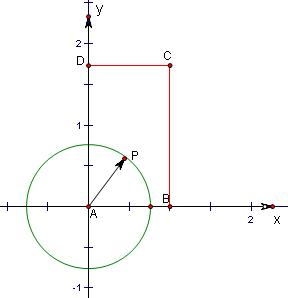
如图所示，在图中，设P（x，y）．

B（1，0），D（0，

3
），C（1，
3
）．

由AP=

3
2
，得x2+y2=
3
4
，

则点P满足的约束条件为

0≤x≤1
0≤y≤
3
x2+y2=
3
4
．

∵

AP
=λ
AB
+μ
AD
即（x，y）=λ（1，0）+μ（0，
3
）

∴x=λ，y=

3
μ，∴λ+
3
μ=x+y．

由于x+y≤

2(x2+y2)
=
2×
3
4
=
6
2
，

当且仅当x=y时取等号．

則λ+

3
μ=x+y的最大值为
6
2
．

故选C．

选择题

观察水边风景照片，会发现“倒影”部分比景物本身暗一些，这是由于（　　）

A．眼睛有一种习惯性感觉

B．入射到水面的光线有一部分进入水中

C．光线被反射掉一部分

D．照片质量有问题
查看答案
单项选择题

患者男性，12岁，6小时前跑步时摔倒，右肘部着地，右肘肿胀压痛，半屈位畸形，前臂明显肿胀，手部皮肤苍白，发凉，麻木，桡动脉搏动微弱，测前臂组织压力60mmHg，X线检查结果为肱骨髁上骨折，应给予的紧急处理为

A．手法复位

B．患肢石膏固定

C．口服利尿剂

D．夹板固定

E．尽快手术
查看答案