问题
解答题
| 等腰直角三角形ABC的斜边BC的长为8，直线MN∥BC且与AB、AC分别交于M、N，将△AMN沿直线MN翻折得△A′MN，设△A′MN与△ABC重合部分面积为y，MN=x， （1）当A′在△ABC内部时，求y与x的函数关系式，并求x的取值范围； （2）是否存在直线MN，使y的值为△ABC面积的
|
答案
（1）y=S△A′MN=
•1 2
x•2 2
x=2 2
x2（0＜x＜4）；1 4
（2）S△ABC=
×8×4=16，当A′在BC上时，x=4，y=4，1 2
∴①当A′在BC边上或在△ABC内部时，0＜y≤4，
不在这个范围内，所以这时不存在直线MN．16 3
②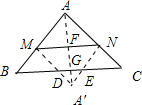
当A′在△ABC外部时，连AA′交MN于F，交BC于G，且A′F=AF=
x，1 2
∴FG=4-
x，1 2
∴A′G=
x-4+1 2
x=x-4，1 2
∴DE=2A′G=2x-8，
∴y=
（x+2x-8）×（4-1 2
x）=-1 2
x2+8x-16（其中4＜x＜8），3 4
当y=
时，16 3
∵-
x2+8x-16=3 4
，16 3
即：（3x-16）2=0，
解为x1=x2=
，16 3
∵4＜x＜8，
∴存在直线MN使重叠部分面积为△ABC面积的
，1 3
此时x=
．16 3