问题
解答题
已知函数f(x)=
(1)求f(x)的表达式; (2)当x∈[0,
|
答案
(1)f(x)=
sinωxcosωx+sin2ωx-3
=1 2
sin2ωx+3 2
-1-cos2ωx 2 1 2
=
sin2ωx-3 2
cos2ωx=sin(2ωx-1 2
).π 6
∵f(x)的周期为π,故T=
=π,∴ω=1,2π 2ω
∴f(x)=sin(2x-
).π 6
(2)由(1)知f(x)=sin(2x-
),当x∈[0,π 6
]时,2x-π 2
∈[-π 6
,π 6
].5π 6
当2x-
∈[-π 6
,π 6
],即x∈[0,π 2
]时,f(x)单调递增;2x-π 3
∈(π 6
,π 2
],5π 6
即x∈(
,π 3
]时,f(x)单调递减;π 2
又f(0)=-
,f(1 2
)=π 2
.1 2
∴f(x)max=f(
)=1,f(x)min=f(0)=-π 3
.1 2

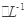 的硝酸溶液中充分反应,产生NO气体,所得澄清溶液成分可看作是Fe(NO3)3、H2SO4的混合液,则反应中未被还原的硝酸可能为( )
的硝酸溶液中充分反应,产生NO气体,所得澄清溶液成分可看作是Fe(NO3)3、H2SO4的混合液,则反应中未被还原的硝酸可能为( )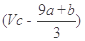 )mol
)mol