问题
填空题
设函数z=f(x，y)的二阶偏导数存在，
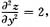且f(x，0)=1，f’(x，0)=x，则f(x，y)=______。
答案
参考答案：z=y2+xy+1
解析：[详解] 由[*]知，[*]由f’y(x，0)=x，得C1(x)=x，于是有[*]=2y+x，从而z=y2+xy+C2(x)，又f(x，0)=1，C2(x)=1，故z=y2+xy+1
搜题请搜索小程序“爱下问搜题”
设函数z=f(x，y)的二阶偏导数存在，
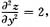且f(x，0)=1，f’(x，0)=x，则f(x，y)=______。
参考答案：z=y2+xy+1
解析：[详解] 由[*]知，[*]由f’y(x，0)=x，得C1(x)=x，于是有[*]=2y+x，从而z=y2+xy+C2(x)，又f(x，0)=1，C2(x)=1，故z=y2+xy+1