问题
计算题
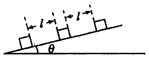
如图所示,倾角为θ的斜面上静止放置三个质量均为m的木箱,相邻两木箱的距离均为l。工人用沿斜面的力推最下面的木箱使之上滑,逐一与其他木箱碰撞。每次碰撞后木箱都粘在一起运动。整个过程中工人的推力不变,最后恰好能推着三个木箱匀速上滑。已知木箱与斜面间的动摩擦因数为μ,重力加速度为g,设碰撞时间极短,求:
(1)工人的推力;
(2)三个木箱匀速运动的速度;
(3)在第一次碰撞中损失的机械能。
答案
解:(1)设工人的推力为F,则有F=3mg(sinθ+μcosθ) ①
(2)设第一次碰撞前瞬间木箱速度为v1,由功能关系得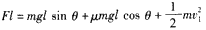 ②
②
设碰撞后两木箱的速度为v2,由动量守恒得mv1=2mv2 ③
设再次碰撞前瞬间速度为v3,由功能关系得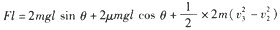 ④
④
设碰撞后三个术箱一起运动的速度为v4,由动量守恒得2mv3=3mv4 ⑤
联立以上各式得 ⑥
⑥
(3)设在第一次碰撞中损失的机械能为△E,有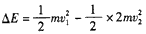 ⑦
⑦
联立①②③⑦式得△E=mgl(sinθ+μcosθ) ④
