问题
问答题
设
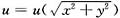具有连续二阶偏导数，且满足
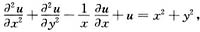
试求函数u的表达式。
答案
参考答案：令[*]则
[*]
同理
[*]
代入原方程，即得
[*]
再解此二阶常系数线性非齐次微分方程，得其通解为
u=C1cosr+C2sinr+r2-2
故函数u的表达式为
[*]
其中C1，C2是任意常数。
解析：
[分析]： 先设[*]然后分别求出[*]代入原方程验证；最后再解微分方程。