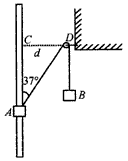
如图所示,光滑固定的竖直杆上套有一个质量m=0.4 kg的小物块A,不可伸长的轻质细绳通过固定在墙壁上、大小可忽略的定滑轮D,连接物块A和小物块B,虚线CD水平,间距d=1.2m,此时连接物块A的细绳与竖直杆的夹角为37°,物块A恰能保持静止。现在物块B的下端挂一个小物块Q,物块A可从图示位置上 升并恰好能到达C处。不计摩擦和空气阻力,cos37°=0.8、sin37°=0.6,重力加速度g取10 m/s2,求:
(1)物块A到达C处时的加速度大小;
(2)物块B的质量;
(3)物块Q的质量。
解:(1)当A物块到达C处时,由受力分析可知:水平方向受力平衡,竖直方向只受重力作用,所以A物块的加速度a=g=10 m/s2
(2)设B物块的质量为M,绳子拉力为T,根据平衡条件有
Tcos37°=mg,T=Mg
联立解得M=0.5kg
(3)设Q物块的质量为m0,根据系统机械能守恒得:
mghac=(M+m0)ghb
hac=dcot37°=1.6m
hb=d/sin37°-d=0.8m
解得:m0=0.3kg
