问题
问答题
根据以下材料回答问题：
某产品过去5年的销售额与目标市场人均收入的数据如表2，预计2006年该产品的目标市场人均收入为1800元。表2 1999～2003年产品销售额与目标市场人均收入
已知数据：1999～2003年产品销售额的平方和为6465；1999～2003年人均收入的平方和为7652500；1999～2003年人均收入与产品销售额乘积之和为222400。
1．建立一元线性回归模型(参数计算结果小数点后保留3位)。
2．进行相关系数检验(取a=0.05，R值小数点后保留3位，相关系数临界值见表3)。
3．对2006年可能的销售额进行点预测。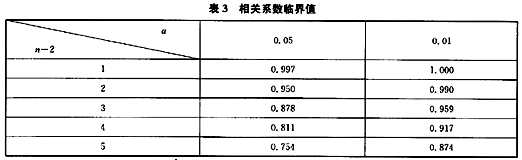
答案
参考答案：
1．建立一元回归模型
首先设该产品销售额为因变量y，设人均收入为自变量x，可以建立一元回归模型：
y=a+bx
其次计算模型的参数：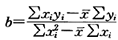 
=(222400-1230×179)/(7652500-1230×6150)=0.025
a=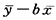 
=35.8-0.025×1230-5.05
最后得到一元回归模型：y=5.05+0.025x
2．相关检验：
则R=0.997
查表可得，当a=0.05时，自由度n-2=5-2=3，得R0.05=0.878
因R=0.997＞0.878=R0.05
故在a=0.05的显著性检验水平上，检验通过，说明人均收入与该产品销售额线性相关的假定是合理的。
3．销售额预测：
已知x2006=1800元
则：y2006=a+bx2006=(5.05+0.025×1800)万元=50.05万元。