问题
解答题
求过点2x+y+8=0和x+y+3=0的交点,且与直线2x+3y-7=0垂直的直线方程。
答案
直线的方程为3x-2y+19=0
解:由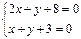 解得交点A(-5,2),
解得交点A(-5,2),
∵所求直线与已知直线2x+3y-7=0垂直
∴可设所求直线的方程为3x-2y+C=0
∵所求直线过交点A(-5,2)
∴3×(-5)-2×2+C=0,∴ C=19
∴所求直线的方程为3x-2y+19=0
求过点2x+y+8=0和x+y+3=0的交点,且与直线2x+3y-7=0垂直的直线方程。
直线的方程为3x-2y+19=0
解:由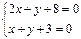 解得交点A(-5,2),
解得交点A(-5,2),
∵所求直线与已知直线2x+3y-7=0垂直
∴可设所求直线的方程为3x-2y+C=0
∵所求直线过交点A(-5,2)
∴3×(-5)-2×2+C=0,∴ C=19
∴所求直线的方程为3x-2y+19=0