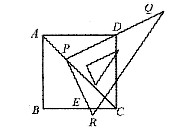
如图所示,在边长为1的正方形ABCD中,一直角三角尺PQR的直角顶点P在对角线AC上移动,直角边PQ经过点D,另一直角边与射线BC交于点E.
(1)试判断PE与PD的大小关系,并证明你的结论;
(2)连接PB,试证明:△PBE为等腰三角形;
(3)设AP=x,△PBE的面积为y,
①求出y关于x的函数关系式;
②当点P落在AC的何处时,△PBE的面积最大,此时最大值是多少
参考答案:
过点P作GF∥AB,分别交AD、BC于G、F.如图所示.
[*]
∵四边形ABCD是正方形,
∴四边形ABFG和四边形GFCD都是矩形,
△AGP和△PFC都是等腰直角三角形.
∴GD=FC=FP,GP=AG=BF,∠PGD=∠PFE=90°
又∵∠1+∠3=∠2+∠3=90°∴∠1=∠2.
又PF=GD,∠PFE=∠PGD=90°,
∴Rt△EFP≌Rt△PGD(ASA).
∴PE=PD.
(2)∵AD=AB,∠PAB=∠PAD=45°,AP=AP,
∴△APB≌△APD(SAS).
∴PB=PD.
∴PE=PB.
∴△PBE为等腰三角形.
(3)①∵AP=x.
[*]
[*]
即当P落在AC的中点处时,△PBE的面积最大,为[*]
