问题
证明题
已知数列{an} 、{bn} 、{cn} ，其中{an} 、{bn} 是等比数列．对于任意正整数n，an、cn、bn 成等差数列，且c1 ≠0 ．试证明：“数列{cn} 是等比数列”的充要条件是“数列{an} 与{bn} 的公比相等”．
答案
证明：充分性：
设数列{an} 与{bn} 的公比都是q ，则an=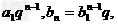
而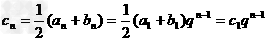
又c1≠0，
故{cn}是公比为q的等比数列．充分性得证．
必要性：
若数列{cn}是等比数列，设数列{an}，{bn}，{cn}的公比分别为p，q，r，则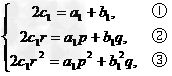
由①×③得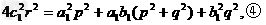
将②的两边平方得
比较④⑤两式得p2+q2=2pq，故p=q，
即数列{an}与{bn} 的公比相等，必要性得证
综上可得，“数列{cn}是等比数列”的充要条件是“数列{an}与{bn}的公比相等”．