问题
解答题
已知△ABC的面积为14cm2,D,E分别为边AB,BC上的点,且AD:DB=BE:EC=2:1,且AE交CD于点P,求△APC的面积.
答案
过E作EF∥AB,交CD于F
∵△BCD中,BE:EC=2:1,∴EF=
BD1 3
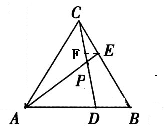
又∵AD:DB=2:1,得BD=
AD1 2
∴EF=
AD1 6
∵△APD∽△EPF,得
=AP PE
=6AD EF
∴AP=6PE,得AP=
AE6 7
∵△APC与△ACE有相同的高,其面积比等于底边的比
∴
=S△APC S△ACE
=AP AE
,得S△APC=6 7
S△ACE6 7
又∵CE=
BC,得S△ACE=1 3
S△ABC=1 3 14 3
∴S△APC=
S△ACE=6 7
×6 7
=4,14 3
即△APC的面积等于4.
