问题
计算题
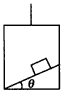
如图所示,在升降机中,质量为m的木块放在倾角为θ、质量为M的斜面上,木块与斜面保持相对静止,分别求以下两种情况中,木块所受到的支持力FN和摩擦力Ff、斜面体对升降机底板的压力F'。
(1)当升降机以速度v匀速上升时;
(2)当升降机以加速度a匀减速上升时。
答案
解:(1)当升降机匀速上升时,M、m均处于平衡状态,如图所示。用隔离法分析木块的受力,应用平衡条件,木块所受到的支持力FN和摩擦力Ff为:FN=mgcosθ,Ff=mgsinθ。用整体法分析M、m组成的系统的受力,再根据牛顿第三定律确定斜面体对底板的压力F'=F=(M+m)g
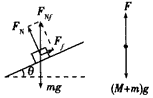
(2)当升降机以加速度a匀减速上升时,加速度的方向竖直向下,合力方向竖直向下,设FN、Ff的合力为FNf,方向竖直向上,由牛顿第二定律得:mg-FNf=ma,则FNf=m(g-a)
由平行四边形得:FN=FNfcosθ=m(g-a) cosθ,Ff=FNfsinθ=m(g-a)sinθ
对M、m组成的系统应用牛顿第二定律得:(M+m)g-F=(M+m)a
则F=(M+m)(g-a)
由牛顿第三定律知F'=F=(M+m)(g-a)
