问题
计算题
如图所示，质量为m1的物体A经一轻质弹簧与下方地面上的质量为m2的物体B相连，弹簧的劲度系数为k，A、B都处于静止状态。一条不可伸长的轻绳绕过轻滑轮，一端连物体A，另一端连一轻挂钩。开始时各段绳都处于伸直状态，A上方的一段绳沿竖直方向。现在挂钩上挂一 质量为m3的物体C并从静止状态释放，它恰好能使B离开地面但不继续上升。已知重力加速度为g，求：
（1）物体C下降的最大距离d；
（2）物体C下降到最低点的过程中弹簧弹性势能的增量△Ep；
（3）若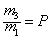
，试讨论当C速度最大时弹簧所处的状态与p值的关系。
答案
解：（1）开始时，A、B静止，设弹簧压缩量为x1，由平衡条件得：kx1=m1g
挂C并释放后，C向下运动，A向上运动，设B刚要离地时弹簧伸长量为x2，则有kx2=m2g
B不再上升表示此时A和C的速度为零，C已降到其最低点
C下降的最大距离为
（2）对A、C、弹簧组成的系统，由能量守恒得
弹簧弹性势能的增量△Ep=m3gd-m1gd
解得
（3）当C速度最大时，A和C的加速度均为零，绳中拉力T=m3g
对A：取向上为正方向，T-m1g+kx=0
解得kx=（m1-m3）g=（1-p）m1g
当p=1时，弹簧处于原长状态；
当p>1时，弹簧处于伸长状态；
当p＜1时，弹簧处于压缩状态