问题
解答题
(1)利用向量有关知识与方法证明两角差的余弦公式:Cα-β:cos(α-β)=cosαcosβ+sinαsinβ;
(2)由Cα-β推导两角和的正弦公式Sα+β:sin(α+β)=sinαcosβ+cosαsinβ.
答案
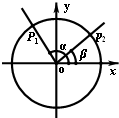
(1)如图,在平面直角坐标系中,以原点为圆心,
作一单位圆,再以原点为顶点,
x轴非负半轴为始边分别作角α,β.
设它们的终边分别交单位圆于点P1(cosα,sinα),P2(cosβ,sinβ),…(4分)
即有两单位向量
,OP1
,OP2
它们的所成角是|α-β|,
根据向量数量积的性质得:
•OP1
=cos(α-β)=cos|α-β|①OP2
又根据向量数量积的坐标运算得:
•OP1 OP2
=cosαcosβ+sinαsinβ②
由①②得 cos(α-β)=cosαcosβ+sinαsinβ…(9分)
(2)sin(α+β)=cos(
-α-β)=cos[(π 2
-α)-β]…(11分)π 2
=cos[(
-α)cosβ+sin(π 2
-β]…(13分)π 2
=cos(
-α)cosβ+sin(π 2
-α)sinβπ 2
=sinαcosβ+cosαsinβ
即有sin(α+β)=sinαcosβ+cosαsinβ…(15分)
