∵5

AP

-2

AB

-

AC

=

0

∴移项化简，可得

AP

=

2

5

AB

+

1

5

AC

因此，设向量

AG

=

2

5

AB

，

AF

=

1

5

AC

，

可得

AP

=

AG

+

AF

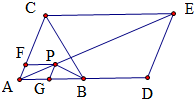
点P在以AG、AF为邻边的平行四边形的第四个顶点处，如图所示

平行四边形ACED中，

AE

=

AC

+

AD

B为AD中点，得

AG

=

1

5

AD

，

∴△PAB的面积S₁=

1

10

S_△ADE=

1

20

S_{平行四边形ACED}

又∵△ABC的面积S₂=

1

4

S_{平行四边形ACED}

∴S₁：S₂=

1

20

：

1

4

=

1

5

，即△PAB的面积与△ABC的面积的比值为

1

5

故选：D