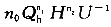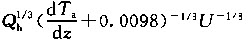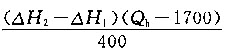问题
解答题
△ABC内接于⊙O:x2+y2=1(O为坐标原点),且3
(1)求△AOC的面积; (2)若
|
答案
(1)∵3
+4OA
+5OB
=0OC
∴3
+4OA
=-5OB OC
据向量加法的平行四边形法则得sin∠AOC=
,cos∠AOC=-4 5 3 5
∴△AOC的面积=
OA•OC•sin∠AOC=1 2 2 5
(2)∵
• OA
=(1,0)•(cos(θ-OC
),sin(θ-π 4
))=cos(θ-π 4
)π 4
∵
•OA
=OC
|||OA
|cos∠AOC═-OC 3 5
∴cos(θ-
)=-π 4 3 5
∵θ∈(-
,0)3π 4
∴θ-
∈(-π,-π 4
)π 4
∴sin(θ-
)=-π 4 4 5
∴sinθ=sin[(θ-
)+π 4
]=sin(θ-π 4
)cosπ 4
+cos(θ-π 4
)sinπ 4
=-π 4 7 2 10