在平面直角坐标系中，A点坐标为（3-2，0），C点坐标为（-3-2，0_爱下问搜题

搜题请搜索小程序“爱下问搜题”

问题解答题

在平面直角坐标系中，A点坐标为（

3

-

2

，0），C点坐标为（-

3

-

2

，0）．B点在y轴上，且S△ABC=

3

．将△ABC沿x轴向左平移

2

个单位长，使点A、B、C分别平移到A′，B′，C′．
（1）画出草图，求B点的坐标；
（2）求A′，B′，C′三点的坐标；
（3）求四边形C′ABB′的面积．

答案

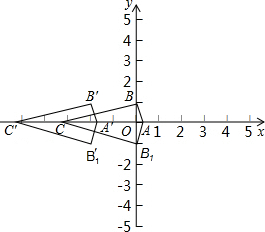
（1）点B有两种情况，一正一负．

故点B的坐标是（0，1）或（0，-1）．

（2）如上图．

A′（

3

-2

2

，0），B′（-

2

，±1）），C′（-

3

-2

2

，0）．

（3）从图可知C′A=|-

3

-2

2

|+

3

-

2

=2

3

+

2

BB′=

2

，

高为1，

∴梯形面积=（2

3

+

2

+

2

）×1÷2=

3

+

2

．

单项选择题

下列协议中（）最消耗CPU与内存资源

A、RIP

B、OSPF

C、SNMP

单项选择题

下列可以视同二手房按揭贷款办理的情况是（）

A.购房人取得产权在六个月之内的（以产权证记载的发证日期为准）

B.购房人取得产权在九个月之内的（以产权证记载的发证日期为准）

C.购房人取得产权在1年之内的（以产权证记载的发证日期为准）

D.购房人取得产权在八个月之内的（以产权证记载的发证日期为准）