问题
解答题
已知，命题p：抛物线C：y=﹣x2+mx﹣1与线段AB：x+y=3（1≤x≤2）有且只有一个交点，命题q：不等式|x﹣m+5|+x≥0的解集为R，问命题p是命题q成立的什么条件？
答案
解：命题p等价于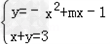 
在[1，2]上只有一个解，
等价于x2﹣（m+1）x+4=0 在[1，2]上只有一个根，
等价于f（x）=x2﹣（m+1）x+4在[1，2]上只有一个零点．
故f（1）f（2）≤0，解得 m≤3 或 m≥4．
命题q等价于函数y=|x﹣（m﹣5）|的图象恒在函数y=﹣x的上方，
等价于m﹣5≥0，解得 m≥5．
显然由命题q成立能推出命题p成立，但由命题p成立不能推出命题q成立．
故命题p是命题q成立的必要不充分条件．