问题
问答题
设A，B分别是m阶与n阶正定矩阵，证明
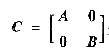是正定矩阵．
答案
参考答案：证法一 由于A，B均是正定矩阵，知AT=A，BT=B，那么
[*]
可知矩阵A的特征值λ1，λ2，…，λm与矩阵B的特征值μ1，μ2，…，μn就是矩阵C的特征值．
因为矩阵A，B均正定，所以λi(i=1，2，…，m)，μj(j=1，2，…，n)均为正数，即矩阵C的特征值全大于零，故矩阵C正定．
证法二 矩阵C对称同前，略．
证法三 C对称同前，略．
因为A，B分别是m阶，n阶正定矩阵，故存在m阶与n阶可逆矩阵D1与D2，使得
[*]
解析：评注 证法一 是用特征值，在证明中是常用的；证法二 是用定义法，应当会用这种方法；证法三 中的充分必要条件A=DTD是考生不熟悉的，但有时候它会比较简单，应知道这种方法。