问题
问答题
设
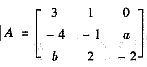，向量
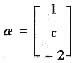是矩阵A-1属于特征值λ0的特征向量，若|A|=-2，求a，b，c及λ0的值．
答案
参考答案：由A-1α=λ0α两边左乘A得λ0Aα=α，即
[*]
则有 a(b-6)=0．
若a=0，由①、②解出c=-2，λ0=1，代入③得b=-2．
若b=6，由①、③解出c=-4，λ0=-1，代入②得a=-2．
解析：评注 虽α是A-1的特征向量誊但不要由A去求A-1那样会很繁琐，用恒等变形转换为A的特征向量会方便得多．
