问题
问答题
已知矩阵
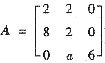 能相似对角化,求正交变换化二次型xTAx为标准形.
能相似对角化,求正交变换化二次型xTAx为标准形.
答案
参考答案:由A的特征多项式[*]
知矩阵A的特征值是λ1=λ2=6,λ3=-2.由于矩阵A可以相似对角化,故λ=6必有2个线性无关的特征向量,那么由
[*]
[*]
知二次型XTAx=XTA1x的特征值是6,7,-3.
对λ=6,由(6E-A)x=0 得 α1=(0,0,1)T.
对λ=7,由(7E-A1)x=0 得 α2=(1,1,0)T.
对λ=-3,由(-3E-A1)x=0 得 α3=(1,-1,0)T.
不同特征值的特征向量已正交,故只需单位化,有
[*]
解析:评注 矩阵A虽不是实对称矩阵,但xTAx仍是二次型,只不过此二次型的矩阵不是A而是A1.
