问题
问答题
设A是3阶实对称矩阵，λ1，λ2，λ3是矩阵A的三个不同的特征值，α1，α2，α3是相应的单位特征向量，证明
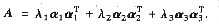
答案
参考答案：令P=(α1，α2，α3)，则P是正交矩阵，由于A是实对称矩阵，故必有
[*]
[*]
搜题请搜索小程序“爱下问搜题”
设A是3阶实对称矩阵，λ1，λ2，λ3是矩阵A的三个不同的特征值，α1，α2，α3是相应的单位特征向量，证明
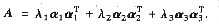
参考答案：令P=(α1，α2，α3)，则P是正交矩阵，由于A是实对称矩阵，故必有
[*]
[*]