问题
单项选择题
已知
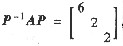α1是矩阵A属于特征值λ=6的特征向量，α2和α3是矩阵A属于特征值λ=2的线性无关的特征向量，如果
①P=(α3，-α2，2α1) ②P=(3α1，α3，α2)
③P=(α2，α2-α3，α1) ④P=(α3，α1+α2，α1)
那么正确的矩阵P是
答案
参考答案：B
解析：[*]是矩阵A的特征值，而α1，α2，α3依次分别是α1，α2，α3的特征向量．
根据特征值，特征向量的性质：
1°若α，β是矩阵A属于特征值λ的特征向量，则kα+lβ(kl≠0)仍是矩阵A属于特征值λ的特征向量．
2°若α，β是矩阵A不同特征值的特征向量，则kα+lβ(kl≠0)就不是矩阵A的特征向量．
因为④中的α1+α2不是矩阵A的特征向量，而②中矩阵P的特征向量的排序与对角矩阵Λ中特征值的排序不协调，故②、④不正确，所以应选(B)．