用括号中所给词的适当形式补全短文。
Where is the best place to live in the United States? Maria: I think San Diego is one of the best 1
(place) to live in the US. It's one of the 2 (safe) cities in America and has very little crime (犯罪). The
schools are good and there are a lot of 3 (university). The weather is the 4 (good) in the country.
It's never too hot or too cold. The views are beautiful here with great beaches and 5 (mountain). The
people are really nice and friendly. There are a lot of immigrants (移民) here so you can 6 (meet)
people from all over the world. The only downside (缺点) is the cost of housing. Many people want
7 (live) here but the high cost of housing stops them.
Daniel: Alabama is a great place to live. In middle Alabama, even in the 8 (cold) days of winter,
the temperature (温度) is still about 40 degrees. In the 9 (hot) days of summer, the temperature is
about 95 degrees. There are great schools in Alabama. Middle Alabama is the 10 (bad) place to take
a vacation, but the best place to live!
|
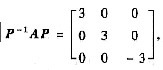 且α1=
且α1=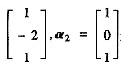 是矩阵A属于特征值λ=3的特征向量,则P=______.
是矩阵A属于特征值λ=3的特征向量,则P=______.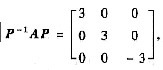 且α1=
且α1=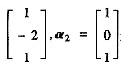 是矩阵A属于特征值λ=3的特征向量,则P=______.
是矩阵A属于特征值λ=3的特征向量,则P=______.