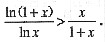问题
问答题
证明：当x＞1时，
答案
参考答案：
证：设F(x)=(1+x)ln(1+x)-xlnx，
F’(x)=ln(1+x)+1-lnx-1
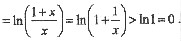
所以，当x＞1时，F’(x)＞0，即F(x)单调增加．
当x＞1时，F(x)＞F(1)=2ln 2＞0，
即(1+x)ln(1+x)-xlnx＞0．
搜题请搜索小程序“爱下问搜题”
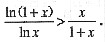
证明：当x＞1时，
参考答案：
证：设F(x)=(1+x)ln(1+x)-xlnx，
F’(x)=ln(1+x)+1-lnx-1
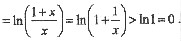
所以，当x＞1时，F’(x)＞0，即F(x)单调增加．
当x＞1时，F(x)＞F(1)=2ln 2＞0，
即(1+x)ln(1+x)-xlnx＞0．