问题
问答题
某工厂要制造一个无盖的圆柱形发酵池，其容积是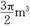
，池底的材料30元/m2，池壁的材料20元/m2，问如何设计，才能使成本最低，最低成本是多少元
答案
参考答案：
设池底半径为r，池高为h(如图所示)，则
，得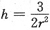
．
又设制造成本为S，则
S=30·πr2+20·27πrh
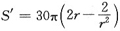
令S’=0，得驻点r=1．
因为
所以r=1为唯一的极小值，即为最小值点．
所以，池底半径为1m，高为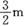
时，可使成本最低，最低成本为90π元．
解析：
本题考查的知识点是应用导数求实际问题的极值．所谓“成本最低”，即求制造成本函数在已知条件下的最小值．因此，本题的关键是正确写出制造成本函数的表达式，再利用已知条件将其化为一元函数，并求其极值．