问题
解答题
| 如图1,在平面直角坐标系中,点A、B的坐标分别为(-1,0)、(3,0),现将线段AB向上平移2个单位,再向右平移1个单位,得到线段CD,连接AC、BD. (1)求点C、D的坐标及四边形ABDC的面积S四边形ABDC; (2)如图2,在y轴上是否存在一点P,连接PA、PB,使S△PAB=S四边形ABDC,若存在这样的一点,求出点P的坐标;若不存在,试说明理由. (3)若点Q在线段CD上移动(不包括C、D两点),QO与线段CD、AB所成的角∠2与∠1如图3所示,给出下列两个结论:①∠2+∠1的值不变,②
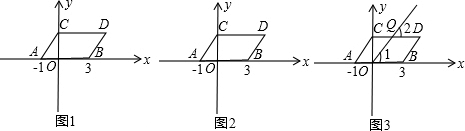 |
答案
(1)C(0,2)D(4,2)(1分)
S四边形ABDC=|AB|•|CO|
=4×2
=8(3分)
(2)假设y轴上存在P(0,b)点,则S△PAB=S四边形ABDC
|AB|•|b|=8,1 2
b=±4,(1分)
∴P(0,4)或P(0,-4),(2分)
(3)②正确
∵CD是由AB平移所得到的,
∴CD∥AB,(1分)
∴∠1=∠2(两直线平行,同位角相等),
∴
=1(恒等于1).(2分)∠1 ∠2
