已知m＞1，直线x-my-m2/2=0，椭圆C：x2/m2+y2=1，F1，F2分别

问题问答题

已知m＞1，直线x-my-m2/2=0，椭圆C：x2/m2+y2=1，F1，F2分别为椭圆C的左、右焦点．

(1)当直线l过右焦点F₂时，求直线l的方程；
(2)设直线l与椭圆C交于A，B两点，△AF₁Fw₂，△BF₁F₂的重心分别为G，H．若原点O。在以线段GH为直径的圆内，求实数m的取值范围．

答案

参考答案：

(1)因为直线l：[*]解得m²=2。

又因为m＞1，所以m=√2

故直线l的方程为x-√2y-√2²/2=0

(2)设A(x₁，y₁)，B(x₂，y₂)，

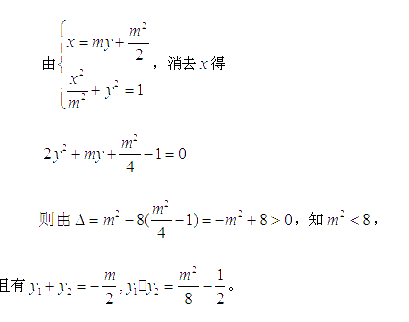
由于F₁(-c，0)，F₂(c，0)，故O为F₁F₂的中点，又因为m＞1且△＞0，所以1＜m＜2．

所以m的取值范围是(1，2)．