问题
问答题
设函数f(x)=-x(x-a)2(x∈R),其中a∈R.
(1)当a=1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)当a≠0时,求函数f(x)的极大值和极小值,
答案
参考答案:
(1)当a=1时,f(x)=-x(x-1)2=-x3+2x2-x,
f(2)=-2,f′(x)=-3x2+4x-1,
f′(2)=-12+8-1=-5,
∴当a=1时,曲线y=f(x)在点(2,f(2))处的切线方程为5x+y-8=0.
(2)f(x)=-x(x-a)2=-x3+2ax2-a2x,
f′(x)=-3x2+4ax-a2=-(3x-a)(x-a),
令f′(x)=0,解得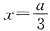 或x=a.
或x=a.
由于a≠0,以下分两种情况讨论,
①若a>0,当x变化时,f′(x)的正负如下表:
因此,函数f(x)在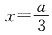 处取得极小值
处取得极小值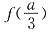 ,且
,且 ,
,
函数f(x)在x=a处取得极大值f(a),且f(a)=0.
②若a<0,当x变化时,f′(x)的正负如下表:
因此,函数f(x)在x=a处取得极小值f(a),且f(a)=0;
函数f(x)在 处取得极大值
处取得极大值 ,且
,且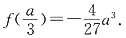

 Mg2+离子中的质子和中子
Mg2+离子中的质子和中子