问题
问答题
已知向量m=(sinA,cosA),n=(1,-2),且m·n=0。
(1)求tanA的值;
(2)求函数f(x)=cos2x+tanAsinx(x∈R)的值域。
答案
参考答案:
由题意得m·n=sinA-2cosA=0。
∵cosA≠0.
∴tanA=2。
(2)由(1)知tanA=2,
所以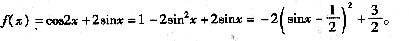
∵x∈R.
∴sinx∈[-1,1]。
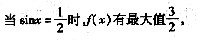
当sinx=-1时,f(x)有最小值-3,
所以函数f(x)的值域是
