问题
计算题
绝缘细绳的一端固定在天花板上,另一端连接着一个电荷量为q、质量为m的小球,当空间加上水平方向的匀强电场后,绳稳定处于与竖直方向成θ=60°角的位置,如图所示.
(1)求匀强电场的场强E;
(2)若细绳长为L,让小球从θ=30°角的A点释放,王明同学求解小球运动至某点的速度的过程如下:
据动能定理mgL(1-cos30°)-qELsin30°=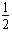 mv2
mv2
得:v=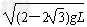
你认为王明同学求的是最低点O还是θ=60°的平衡位置处的速度?正确吗?请详细说明理由或求解过程.

答案
解:(1)当θ=60°时,小球处于平衡状态,由物体的平衡条件得:
FTcosθ=mg
FTsinθ=qE
且θ=60°
解得:E=
(2)王明同学求的应是最低点O处的速度,并且计算不正确
因为当小球由θ=30°处释放后,小球只能绕θ=60°的平衡位置处做往复运动,不可能到达最低点O
由θ=30°处到θ=60°的平衡位置处,根据动能定理得:
qEL(sin60°-sin30°)-mgL(cos30°-cos60°)= mv2
mv2
得:v=
