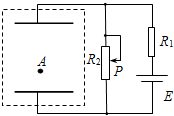
在如图所示的装置中,电源电动势为E,内阻不计,定值电阻为R1,滑动变阻器总值为R2,置于真空中的平行板电容器水平放置,极板间距为d.处在电容器中的油滴A恰好静止不动,此时滑动变阻器的滑片P位于中点位置.
(1)求此时电容器两极板间的电压;
(2)求该油滴的电性以及油滴所带电荷量q与质量m的比值;
(3)现将滑动变阻器的滑片P由中点迅速向上滑到某位置,使电容器上的电荷量变化了Q1,油滴运动时间为t,再将滑片从该位置迅速向下滑动到另一位置,使电容器上的电荷量又变化了Q2,当油滴又运动了2t的时间,恰好回到原来的静止位置.设油滴在运动过程中未与极板接触,滑动变阻器滑动所用时间与电容器充电、放电所用时间均忽略不计.求:Q1与Q2的比值.
(1)电路中的电流I=E R1+ R2 2
平行板电容器两端的电压U=
=
ER2 2 R1+ R2 2
E.R2 2R1+R2
(2)电容上板速写正电,油滴处于静止状态,电场力向上,则油滴带负电.对油滴受力分析,得F电-mg=0,即
=mg,所以
ER2q1 2 (R1+
)dR2 2
=q m
.gd(2R1+R2) ER2
(3)设电容器的电容为C,极板原来具有的电荷量为Q,电容器上的电量变化Q1后,油滴在电场中向上做初速度为零的匀加速直线运动,t秒末油滴的速度为v1、位移为s,板间的电压
U1=Q+Q1 C
根据牛顿第二定律得
F电1-mg=ma1,
-mg=ma1(Q+Q1)q Cd
根据运动学公式得s=
a1t2,v1=a1t1 2
电容器上的电量又变化了Q2后,油滴在电场中向上做匀减速直线运动,2t秒末位移为-s.
极板间的电压为U2=Q+Q1+Q2 C
根据牛顿第二定律得
mg-F电2=ma2,mg-
=ma2(Q+Q1-Q2)q Cd
根据运动学公式得-s=2v1t-
a2(2t)21 2
解得:
=Q1 Q2
.4 9
答:(1)此时电容器两极板间的电压为
E. R2 2R1+R2
(2)油滴带负电,油滴所带电荷量q与质量m的比值为
.gd(2R1+R2) ER2
(3)Q1与Q2的比值为4:9.
