问题
问答题
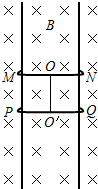
两根可以滑动的金属杆MN、PQ，套在两根竖直光滑轨道上，放置在匀强磁场中，磁场方向垂直导轨平面（纸面）向里，两金属杆MN、PQ的长均为20cm，质量均为0.12kg，电阻均为0.1Ω，导轨电阻不计．用长0.5m的绝缘细线OO′将两金属杆相连，如图所示．
（1）保持回路MNQP的面积不变，当磁场的磁感应强度以2T/s的变化率均匀减小时，求回路中感应电流的大小．
（2）保持磁场的磁感应强度1T不变，将细线OO′剪断，同时用外力使金属杆MN以5m/s的速度竖直向上作匀速运动，试问金属杆PQ最终向什么方向以多大的速度做匀速运动？（设在竖直方向上轨道足够长，磁场范围足够大）
答案
（1）利用法拉第电磁感应定律E=
，△φ △t
得，E=
S△B △t
代入已知量，得E=2×0.5×0.2=0.2V
I=
=E R
=1A0.2 0.2
（2）假设PQ向下匀速运动
对于MN、PQ两棒反向匀速切割磁感线的运动，有E'=BL（v1+v2），
I′=
，E′ R
F'=BI'L，
得F′=
，B2L2(v1+v2) R
对于PQ棒的平衡状态，有F'=G，
则
=G，B2L2(v1+v2) R
代入已知量，得
=1.2，12×0.22×(5+v2) 0.1+0.1
解得v2=1m/s
答：（1）保持回路MNQP的面积不变，当磁场的磁感应强度以2T/s的变化率均匀减小时，则回路中感应电流的大小为1A．
（2）保持磁场的磁感应强度1T不变，将细线OO′剪断，同时用外力使金属杆MN以5m/s的速度竖直向上作匀速运动，则金属杆PQ最终向下方向以1m/s的速度做匀速运动．