问题
问答题
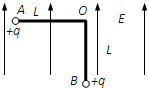
两个带电量均为+q小球，质量均为m，固定在轻质绝缘直角框架OAB（框架的直角边长均为L）的两个端点A、B上，另一端点用光滑铰链固定在O点，整个装置可以绕垂直于纸面的水平轴在竖直平面内自由转动．
（1）若施加竖直向上的匀强电场E1，使框架OA边水平、OB边竖直并保持静止状态，则电场强度E1多大？
（2）若改变匀强电场的大小和方向（电场仍与框架面平行），为使框架的OA边水平、OB边竖直（B在O的正下方），则所需施加的匀强电场的场强E2至少多大？方向如何？
（3）若框架处在匀强电场E1中OA边水平、OB边竖直并保持静止状态时，对小球B施加一水平向右的恒力F，则小球B在何处时速度最大？最大值是多少？
答案
（1）根据有固定转动轴物体的平衡条件，有q
L=mgLE 1
可得
=E 1 mg q
即电场强度
大小为E 1
．mg q
（2）设匀强电场E2的方向与竖直方向夹角为θ，则有力矩平衡条件可得
Lcosθ+qE 2
Lsinθ=mgLqE 2
2
sin(θ+β)，其中tanβ=qE 2
=1，所以β=45°，即1 1 2
sin(θ+qE 2
)=mgπ 4
可见当θ=
时，最小电场强度π 4
=E 2min
mg2 2q
即则所需施加的匀强电场的场强E2至少
，方向与竖直方向成45°角向上．
mg2 2q
（3）由于q
=mg，当OB边右侧水平时B速度最大，由动能定理E 1
有FL=
2mv21 2
可得B球的最大速度为v=FL m
即小球B在水平位置时速度最大，最大速度为v=
．FL m