问题
问答题
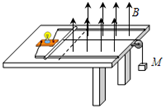
水平桌面上固定两根相距L的足够长的平行光滑金属导轨,导轨左端如图连接一盏阻值为R的小灯泡.垂直导轨放置一根内阻为r的金属棒,金属棒的质量为m,导轨电阻不计.金属棒用绝缘细线通过光滑定滑轮与悬挂于桌外质量为M的重物相连,金属棒可在重物作用下沿导轨平移.整个装置放在一有界匀强磁场中,图中虚线左侧无磁场,右侧磁场方向竖直向上,磁感应强度为B.现将金属棒从静止释放,当金属棒速度达到v0时,刚好进入磁场,此时小灯泡正常发光.此后金属棒做减速运动,最终匀速.求:
(1)金属棒从静止释放到刚进入磁场所运动的时间t.
(2)金属棒刚进入磁场时小灯泡的功率;
(3)金属棒最终做匀速直线运动的速率.
答案
(1)以金属棒和相连重物为研究对象,由牛顿第二定律得 Mg=(M+m)a
因棒做匀加速运动,则有 v0=at
解得,t=(M+m)v0 Mg
(2)金属棒刚进入磁场时产生的电动势 E=BLv0
电路中的电流 I=
=E R+r BLv0 R+r
小灯泡的功率:P=I2R=B2L2
Rv 20 (R+r)2
(3)金属棒做匀速直线运动时 F安=Mg
其中 F安=BI′L=B
L=BLv R+r B2L2v R+r
v=Mg(R+r) B2L2
答:
(1)金属棒从静止释放到刚进入磁场所运动的时间t为
.(M+m)v0 Mg
(2)金属棒刚进入磁场时小灯泡的功率为
;B2L2
Rv 20 (R+r)2
(3)金属棒最终做匀速直线运动的速率为
.Mg(R+r) B2L2
