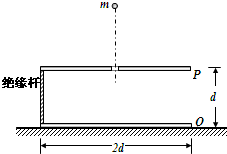
如图所示,完全相同的金属板P、Q带等量异种电荷,用绝缘杆将其连成一平行正对的装置,放在绝缘水平面上,其总质量为M,两板间距为d,板长为2d,在P板中央位置处有一小孔.一质量为m、电量为+q的粒子,从某一高度下落通过小孔后进入PQ,恰能匀速运动.外部的电场可忽略,板间电场可视为匀强电场,重力加速度为g,求:
①PQ间电场强度及电势差;
②粒子下落过程中,装置对绝缘水平面的压力;
③现给PQ间再加一垂直纸面向里、磁感应强度B的匀强磁场,要使粒子进入PQ后不碰板飞出,则粒子应距P板多高处自由下落?
①因小球受力平衡,mg=qE 得:E=
电场方向向上 mg q
PQ间的电势差U=Ed=mgd q
②在小球未进入PQ前对地的压力N1=Mg
进入PQ后小球受到向上大小等于mg的电场力,根据牛顿第三定律可得PQ对地的压力
N2=Mg+mg
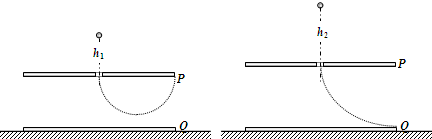
③依题意得:当粒子轨迹恰好与P板右边缘相切时,粒子圆周运动的半径R1=d 2
根据qv1B=m
得v1=v 21 R1 qBR1 m
又由机械能守恒定律得mgh1=
m1 2 v 21
联立解得h1=q2B2d2 8m2g
当粒子轨迹恰好与Q板右边缘相切时,粒子圆周运动的半径R1=d,同理可得 v2=qBR2 m
h2=q2B2d2 2m2g
故要使粒子进入PQ后不碰板飞出,粒子应距P板
<h<q2B2d2 8m2g
高处自由下落.q2B2d2 2m2g
答:①PQ间电场强度E=
,方向向上;电势差为mg q
;mgd q
②在小球未进入PQ前对地的压力N1=Mg
进入PQ后PQ对地的压力N2=Mg+mg;
③要使粒子进入PQ后不碰板飞出,粒子应距P板
<h<q2B2d2 8m2g
高处自由下落.q2B2d2 2m2g
