如图所示,在足够长的光滑水平轨道上静止三个小木块A、B、C,质量分别为mA=1kg,mB=1kg,mC=2kg,其中B与C用一个轻弹簧固定连接,开始时整个装置处于静止状态;A和B之间有少许塑胶炸药,A的左边有一个弹性挡板(小木块和弹性挡板碰撞过程没有能量损失).现在引爆塑胶炸药,若炸药爆炸产生的能量有E=9J转化为A和B沿轨道方向的动能,A和B分开后,A恰好在B、C之间的弹簧第一次恢复到原长时追上B,并且与B发生碰撞后粘在一起.求:

(1)在A追上B之前弹簧弹性势能的最大值;
(2)A与B相碰以后弹簧弹性势能的最大值.
(1)3J;(2)0.5J
(1)塑胶炸药爆炸瞬间取A和B为研究对象,假设爆炸后瞬间A、B的速度大小分别为vA、vB,取向右为正方向
由动量守恒:-mAvA+mBvB=0
爆炸产生的热量由9J转化为A、B的动能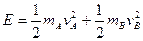
代入数据解得vA =vB =3m/s
由于A在炸药爆炸后再次追上B的时候弹簧恰好第一次恢复到原长,则在A追上B之前弹簧已经有一次被压缩到最短(即弹性势能最大),爆炸后取B、C和弹簧为研究系统,当弹簧第一次被压缩到最短时B、C达到共速vBC,此时弹簧的弹性势能最大,设为Ep1.
由动量守恒,得mBvB=(mB+mC)vBC
由机械能守恒,得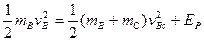
代入数据得EP1=3J
(2)设B、C之间的弹簧第一次恢复到原长时B、C的速度大小分别为vB1和vC1,则由动量守恒和能量守恒:
mBvB=mBvB1+mCvC1

代入数据解得:vB1=-1m/s,vC1=2m/s
(vB1 =3m/s,vC1=0m/s不合题意,舍去.)
A爆炸后先向左匀速运动,与弹性挡板碰撞以后速度大小不变,反向弹回.当A追上B,发生碰撞瞬间达到共速vAB
由动量守恒,得mAvA+mBvB1=(mA+mB)vAB
解得vAB =1m/s
当A、B、C三者达到共同速度vABC时,弹簧的弹性势能最大为EP2
由动量守恒,得(mA+mB)vAB+mCvC1=(mA+mB+mC)vABC
由能量守恒,得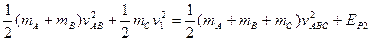
代入数据得EP2 =0.5J
