（1）求物体1从释放到与物体2相碰的过程中，滑道向左运动的距离；
（2）若CD＝0.1m，两物体与滑道的CD部分的动摩擦因数都为μ＝0.1，求在整个运动过程中，弹簧具有的最大弹性势能；
（3）物体1、2最终停在何处。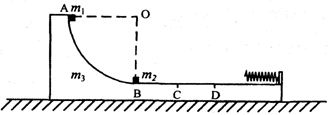
（1）0.05m（2）0.45J （3）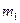
、
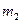最终停在CD的中点处
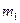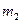（1）从释放到与相碰撞过程中，、
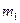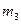组成的系统水平方向动量守恒，设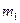水平位移大小
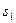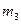，水平位移大小
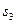，有：
--------------------------------------（2分）
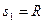--------------------------------------------------（1分）
可以求得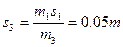
--------------------------------（2分）
（2）设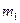、 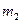刚要相碰时物体1的速度
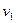，滑道的速度为
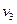，由机械能守恒定律有
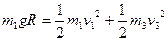-----------------------------（2分）
由动量守恒定律有
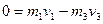---------------------------------------------------（2分）
物体1和物体2相碰后的共同速度设为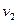
，由动量守恒定律有
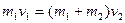-------------------------------------（2分）
弹簧第一次压缩最短时由动量守恒定律可知物体1、2和滑道速度为零，此时弹性势能最大，设为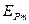
。从物体1、2碰撞后到弹簧第一次压缩最短的过程中，由能量守恒有
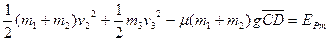------------（3分）
联立以上方程，代入数据可以求得，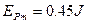
---------------------（2分）
⑶分析可知物体1、2和滑道最终将静止，设物体1、2相对滑道CD部分运动的路程为s，由能量守恒有
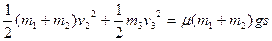-----------------------------（3分）
带入数据可得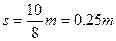
所以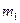、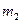最终停在CD的中点处 --------------------------------------（2分）