在光滑的水平面上沿直线按不同的间距依次排列着质量均为m的滑块，1、2、3、…（n－1）、n，滑块P的质量也为m．P从静止开始在大小为F的水平恒力作用下向右运动，经时间T与滑块1碰撞，碰撞后滑块便粘连在一起．以后每经过时间T就与下一滑块碰撞一次，每次碰撞后均粘连在一起，每次碰撞时间极短，每个物块都可简化为质点．求：
 |
（1）第一次碰撞后瞬间的速度及第一次碰撞过程中产生的内能；
（2）发生第n次碰撞后瞬间的速度vn为多大；
（3）第n－1个滑块与第n个滑块间的距离sn-1．
（1）
；（2）
；（3）
（1）设第一次碰撞前瞬间P的速度为u1，根据动量定理，有
FT=mu1 ①
则撞前瞬间的速度u1=
②
因碰撞时间极短，第一次碰撞后瞬间的速度为v1，根据动量定理，有
FT=2mv1 ③
则碰后瞬间速度v1=
④
第一次碰撞过程中产生的内能△E=
= ⑤
（2）因每次碰撞时间极短，对从开始到发生第n次碰撞后瞬间应用动量定理，有
FnT=（n+1）mvn ⑥
解得vn= ⑦
（3）同理可以求出第（n－1）次碰后的速度vn-1=
⑧
对第n次碰撞前全过程应用动量定理
FnT=nmun ⑨
解得un= ⑩（与n无关）
对n－1到n之间应用动能定理，有
Fsn-1=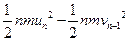
解得sn-1=