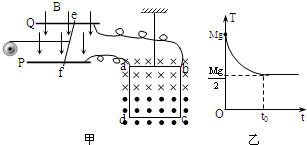
如图甲所示,P、Q为水平面内平行放置的金属长直导轨,间距为d,处在大小为B、方向竖直向下的匀强磁场中.一根质量为m、电阻为r的导体棒ef垂直于P、Q放在导轨上,导体棒ef与P、Q导轨之间的动摩擦因数为μ.质量为M的正方形金属框abcd,边长为L,每边电阻均为r,用细线悬挂在竖直平面内,ab边水平,线框的a、b两点通过细导线与导轨相连,金属框上半部分处在大小为B、方向垂直框面向里的匀强磁场中,下半部分处在大小也为B,方向垂直框面向外的匀强磁场中,不计其余电阻和细导线对a、b点的作用力.现用一电动机以恒定功率沿导轨方向水平牵引导体棒ef向左运动,从导体棒开始运动计时,悬挂线框的细线拉力T随时间的变化如图乙所示,求:
(1)t0时间以后通过ab边的电流;
(2)t0时间以后导体棒ef运动的速度;
(3)电动机的牵引力功率P.
(1)以金属框为研究对象,从t0时刻开始拉力恒定,故电路中电流恒定,设ab边中电流为I1,cd边中电流为I2
由受力平衡:BI1L+T=Mg+BI2L
由图象知T=Mg 2
ad、dc、cb三边电阻串联后再与ab边电阻并联构成,
所以I1:I2=3:1
I1=3I2
由以上各式解得:I1=3Mg 4BL
(2)设总电流为I,由闭合路欧姆定律得:
I=E R+r
R=
r3 4
E=Bdv
I=I1+I2=
I1=4 3 Mg BL
解得:v=7Mgr 4B2dL
(3)由电动机的牵引功率恒定 P=F?v
对导体棒:F=μmg+BId
解得:P=
(μmgL+Mgd)7Mgr 4B2L2d
答:(1)t0时间以后通过ab边的电流是
;3Mg 4BL
(2)t0时间以后导体棒ef运动的速度是
;7Mgr 4B2dL
(3)电动机的牵引力功率是
(μmgL+Mgd).7Mgr 4B2L2d
