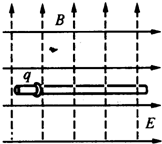
如图所示,在空间存在着水平向右、场强为E的匀强电场,同时存在着竖直向上、磁感应强度为B的匀强磁场.在这个电、磁场共存的区域内有一足够长的绝缘杆沿水平方向放置,杆上套有一个质量为m、带电荷量为+q的金属环.已知金属环与绝缘杆间的动摩擦因数为μ,且μmg<qE.现将金属环由静止释放,设在运动过程中金属环所带电荷量不变.
(1)试定性说明金属环沿杆的运动情况;
(2)求金属环运动的最大加速度的大小;
(3)求金属环运动的最大速度的大小.
(1)金属环在电场力和摩擦力的共同作用下由静止开始做加速运动.随着速度的增大,洛伦兹力从零逐渐增大,金属环所受的摩擦力逐渐变大,合外力减小.所以金属环将做一个加速度逐渐减小的加速运动,达到最大速度vmax后做匀速运动.
(2)开始时金属环速度为零,所受的摩擦力最小,此时金属环所受的合外力最大,根据牛顿第二定律,得
qE-μmg=mamax
得金属环的最大加速度为:amax=qE-mg m
(3)当摩擦力f′=qE时,金属环所受的合外力为零,金属环达到最大速度vmax,则此时所受的洛伦兹力为F洛=Bqvmax,方向垂直纸面向外.
因此,杆对金属环的弹力为N′=(mg)2+(Bqvmax)2
当金属环达到最大速度时有 μ
=qE(mg)2+(Bqvmax)2
解得:vmax=(qE/μ)2-(mg)2 Bq
答:
(1)金属环将做加速度逐渐减小的加速运动,达到最大速度vmax后做匀速运动.
(2)金属环运动的最大加速度的大小amax=
;qE-mg m
(3)金属环运动的最大速度的大小vmax=
.(qE/μ)2-(mg)2 Bq
